Reglas de Simplificacion

Reglas de simplificaciones

Son reglas que se utilizan tanto en el álgebra booleana como en la lógica proposicional que ayuda a reducir en al máximo la mayor cantidad de Operadores lógicos que se encuentran dentro de una función algebraica o una función lógica proposicional para ambos casos se utilizan las mismas solo que cambia la sintaxis

Formas Normales, Inferencias , Tablas de Karnaugh

Existen dos formas normales que se utilizan en la lógica proposicional 

Forma Normal Conjuntiva

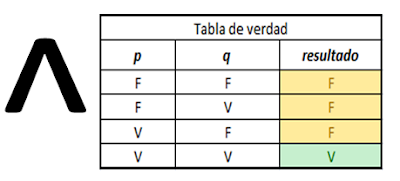
Un polinomio esta de forma normal conjuntiva si el operador de primera instancia (el que une las preposiciones) es la disyunción y el operador que liga los monomios es la conjunción

Una tabla de verdad esta en forma normal conjuntiva si en su salida la cantidad minima de términos es falsa, esta escribe el polinomio de forma normal conjuntiva afirmando las preposiciones que son falsas y negando las verdaderas

Forma Normal Disyuntiva

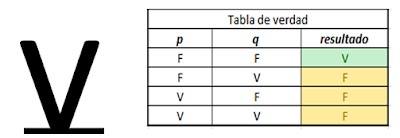
Un polinomio esta de forma normal Disyuntiva si el operador de primera instancia (el que une las preposiciones) es la conjunción y el operador que liga los monomios es la disyunción, es lo contrario a la F.N.C

Una tabla de verdad esta en forma normal Disyuntiva si en su salida la cantidad minima de términos es verdadera, esta escribe el polinomio de forma normal conjuntiva afirmando las preposiciones que son falsas y negando las verdaderas

                                     

Inferencias

Son formas del pensamiento donde prima la validez de las premisas sobre la valide de las proposiciones bajo algunas condiciones

•         Las premisas han de ser verdaderos
•         Se toma para su estudio las tablas de la implicación y la disyunción

Modus Ponendo Poness (Afirmando afirmas)

Si una implicación es verdadera y su antecedente es verdadero entonces el consiente debe ser verdadero

Modus Tallendo Tallens (negando niega)

Si una implicación es verdadera y su antecedente es falso entonces el cociente debes ser falso

Modus Tallendo Poness ( Negando afirma)

Si una implicación es verdadera y una de sus proposiciones es  falsa entonces el cociente debes ser falso, entonces la otra proposición es verdadera

Tabla de Karnaugh

Es un diagrama utiliza para la simplificacion de funciones de caracter algabraica booleanas y lleva dicho nombre gracias al Maurice Karnaugh, dicho diagrama es una representacion gráfica de como se construye una función de algebra Booleana por medio de tablas que el mismo profesor Karnaugh creo, la idea de este mapa es mostrar la forma mas practica y rapida de crear la funcion por medio la escogencia de los valores verdaderos y construir por medio de cruce entre los valores 

Mas información Sobre Karnaugh aqui

Algebra Booleana

Álgebra Booleana

Es una estructura algebraica que esquematiza las operaciones lógicas (  Y ,  O ,   NO ,   SI,    AND ,   OR ,   NOT ,  IF) así como el conjunto de operaciones unión intersección y complemento

Existen las mismas tres característica del álgebra Booleana

•       El verdadero y el falso (Equivalen a  1 - 0 )
•       P , q , r  ( Equivalen a A , B , C )
•       No utiliza arboles sino circuitos  

Es  el mismo proceso que se utiliza en la lógica proposicional lo único que cambia es la sintaxis como se puede ver .

Utiliza la mismas reglas de simplificación y las formas normales que se utilizan en la lógica propisicional

Operadores (Lógica Proposicional)

Operadores

1. Negación :    no 
   
    
2. Conjunción    y
   
   
3.  Conjunción Negado
   
   
   
4. Disyunción
   
   
5. Disyunción Negado
   
   
   
6. Implicación
   
   
7. Implicación Contraria
   
   
   
8. Implicación Negada
   
   
9. Implicación Contraria Negada
   
   
   
10. Bicondicional

Logica Proposicional

Lógica Proposicional

La lógica proposicional también llamada lógica simbólica o lógica matemática es aquella que parte de la lógica y estudia la lógica y símbolos utilizados en la vinculación de nuevas proposiciones que podrían ser verdaderos o falsa, basándose siempre entre dos opciones como variables de respuestas.

Sinos remontamos a la historia fue en el siglo IV con aristoteles que argumento en su libro ORGANON que los juicios están atados entre el raciocinio y a su ves por los conceptos que se infieren, dando como principio de la lógica la identidad humana y el principio de la no contradicción, debió pasar mucho mas tiempo hasta que el señor Boole D'morgan nos habla de comos como la matemática moderna, la famosa álgebra booleana, las teorías de los conjuntos y la LÓGICA PROPOSICIONAL

Como se menciono en su momento la lógica proposicional puede verse como modelo matemático con tres factores importantes

1. Variables, constantes  y números
2. Operadores ( Símbolos de operaciones )
3. Reglas de las operaciones

Operandos

Letras Proposicionales = p , q , r , s , t , u , v , w , x    donde cualquiera de esa letras puede representar una argumento ya sea falso o verdadero

p = "El hombre llego a la luna"

q = "Marte es el noveno planeta del sistema solar"

Bienvenidos a Matematicas Discretas

Esta es una pequeña introducción o bienvenida a lo que recreara esta bellisimo blog de información, el cual esta relacionado no solo con matemáticas discretas sino a mucho ámbitos tecnológicos e informáticos, déjese guiar por este maravilloso mundo de innovacion, descubirmiento y conocemiento en el que juntos podremos conocer que es todo este entorno que nos brinda la ingeniería de sistema, con el apoyo de la educación superior de la universidad ECCI

Matemáticas Discretas

Integrantes del Grupo

Carlos Alexis Garcia Diaz (27894)
Julian Andres Gonzalez  Fuquene (41536)